factor_analysis是一款基于Python的单因子测试框架,为寻找能有效区分和预测股票收益的因子提供标准化的工作流程和实现工具。该框架主要包括数据清洗与因子测试两部分。其中,数据清洗将实现对原始因子数据中异常值和缺失值的处理,以及因子标准化,从而保证后续检验模型的稳健性;因子测试提供三类因子测试模型,帮助投资者从实证角度验证因子有效性,分别为回归检验、投资组合排序法以及信息系数评估。
本页主要介绍以上所提到的因子测试模型的函数使用方法。
Fama-MacBeth回归法
factor_analysis类提供 factor_fm_summ方法,支持Fama-MacBeth回归验证因子有效性。检验因子前,需要指定定价模型(默认为FF-3模型,可选CAPM)。考虑到异方差问题和残差自相关问题,回归系数的标准误将通过Newey-West修正(默认lag为5)。判断候选因子是否有效需检验该因子能否在定价模型因子基础上提供解释股票之间收益率差异的增量信息,即检验候选因子在FM回归中斜率系数是否显著不等于0。
接口:factor_fm_summ
描述:给定定价模型,利用FM回归检验潜在异象因子是否提供解释股票之间收益率差异的增量信息。
输入参数:
| 名称 | 类型 | 必选 | 描述 |
|---|---|---|---|
pricing_model |
str | Y | 定价模型,默认’FF-3’,即Fama-French三因子模型;可选’CAPM’,即资本资产定价模型 |
输出参数:
Fama-MacBeth回归估计结果梗概,包括回归系数、显著性检验与拟合优度等统计量信息。
使用样例
# Fama-MacBeth regression
fa.factor_fm_regr_summ(pricing_model = 'FF-3')
FamaMacBeth Estimation Summary
=====================================================================================
Dep. Variable: returns R-squared: 0.0031
Estimator: FamaMacBeth R-squared (Between): -0.0558
No. Observations: 215554 R-squared (Within): 0.0057
Date: Fri, Jan 14 2022 R-squared (Overall): 0.0031
Time: 04:00:13 Log-likelihood 1.29e+05
Cov. Estimator: Fama-MacBeth Kernel Cov
F-statistic: 166.72
Entities: 4200 P-value 0.0000
Avg Obs: 51.322 Distribution: F(4,215549)
Min Obs: 1.0000
Max Obs: 143.00 F-statistic (robust): 23.893
P-value 0.0000
Time periods: 143 Distribution: F(4,215549)
Avg Obs: 1507.4
Min Obs: 426.00
Max Obs: 2394.0
Parameter Estimates
===============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-------------------------------------------------------------------------------
const 0.0820 0.0270 3.0345 0.0024 0.0290 0.1350
factor -0.0081 0.0009 -9.0512 0.0000 -0.0098 -0.0063
beta 0.0009 0.0032 0.2681 0.7886 -0.0055 0.0072
circ_mc_log -0.0056 0.0018 -3.0357 0.0024 -0.0092 -0.0020
ep_ttm 0.0304 0.0330 0.9226 0.3562 -0.0342 0.0950
===============================================================================
Barra回归法
factor_analysis类提供factor_barra_regr_summ方法,支持Barra回归方法验证因子有效性,包括计算因子每期收益、因子收益率序列t检验、有效因子分类等。单因子回归验证风格因子有效性时,每个换仓期期初的公司特征作为因子暴露,与行业因子(0-1哑变量)和市值因子共同作为回归式的解释变量,换仓期期初至期末的个股收益作为响应变量,以流通市值为权重利用加权最小二乘法回归(WLS)拟合得到的斜率项即为因子在该换仓期的因子收益。在进行因子收益率序列检验时,通过对多期因子收益进行t-检验,将获得t值序列及相关统计指标,从而对因子的有效性、稳定性与方向一致性等性质进行验证。
接口:factor_barra_regr_summ
描述:利用Barra回归检验因子是否预测不同股票之间的收益率差异。
输入参数:
| 名称 | 类型 | 必选 | 描述 |
|---|---|---|---|
industry_neutral |
bool | Y | 是否行业中性化,默认为True |
mkt_cap_neutral |
bool | Y | 是否市值中性化,默认为True |
输出参数:
Barra回归估计结果梗概,包含不同换仓期横截面回归计算所得的平均因子收益率、因子收益率t检验、因子收益率显著性等统计量。
使用样例
# statistics on factor return series
fa.factor_barra_regr_summ(industry_neutral=True,mkt_cap_neutral=True)
Cross-Sectional Regression Summary
=========================================================
Start Date: 2010-01-29 Mean Factor Return: 0.0023
End Date: 2021-09-30 T-stats of Factor Return: 1.3428
Frequency: Monthly Prob. Factor Return > 0: 0.5248
No. Turnover: 141 Absolute Mean t: 5.4255
Prob. Significant t: 0.7518
---------------------------------------------------------
时序回归法
factor_analysis类提供 factor_ts_regr_summ()方法,支持时间序列回归检验因子。回归方程式中,由异象变量(anomaly variables)构建的多空组合收益率将作为被解释变量,指定的定价模型(默认FF-3,可选CAPM,FF-5模型)的因子收益率将作为解释变量,通过对截距项进行t-检验判断异象因子是否有效。t-检验时,考虑到回归式中的残差项的异方差和自相关问题,将通过Newey-West修正标准误估计。其中,在考虑定价模型因子收益率时,可选择剔除科创版与创业板股票(默认包括科创版与创业板),利用Double Sorting方法(默认2×3组合划分方法,可选2×2)与流通市值加权方式计算定价因子收益率。
接口:factor_ts_regr_summ
描述:给定定价模型,利用时间序列回归检验潜在异象因子是否提供解释股票之间收益率差异的增量信息。
输入参数:
| 名称 | 类型 | 必选 | 描述 |
|---|---|---|---|
pricing_model |
str | Y | 定价模型,默认为’FF-3’,即Fama-French三因子模型;可选’FF-5’即五因子模型;可选’CAPM‘,即资本资产定价模型 |
kechuangchuangye |
bool | Y | 定价模型因子收益率是否考虑科创版和创业版股票,默认为True |
portfolio_method |
str | Y | 定价模型因子多空组合划分方式,默认为’2$\times$3’,即以FF模型2×3双排序组合划分方法构建多空组合 |
输出参数:
时间序列回归估计结果梗概,包括回归系数、显著性检验与拟合优度等统计量信息。
使用样例
# time-series regression
fa.factor_ts_regr_summ(pricing_model='FF-3',kechuangchuangye=True,portfolio_method='2*3')
OLS Regression Results
==============================================================================
Dep. Variable: returns R-squared: 0.686
Model: OLS Adj. R-squared: 0.674
Method: Least Squares F-statistic: 47.44
Date: Fri, 14 Jan 2022 Prob (F-statistic): 2.87e-28
Time: 04:09:32 Log-Likelihood: 269.46
No. Observations: 143 AIC: -526.9
Df Residuals: 137 BIC: -509.1
Df Model: 5
Covariance Type: HAC
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
const -0.0179 0.003 -5.818 0.000 -0.024 -0.012
RiskPremium 0.2294 0.067 3.446 0.001 0.098 0.361
SMB 0.5123 0.162 3.161 0.002 0.192 0.833
HML -0.2333 0.180 -1.297 0.197 -0.589 0.122
RMW -0.8605 0.323 -2.663 0.009 -1.499 -0.222
CMA -0.5015 0.214 -2.342 0.021 -0.925 -0.078
==============================================================================
Omnibus: 4.283 Durbin-Watson: 2.104
Prob(Omnibus): 0.118 Jarque-Bera (JB): 3.755
Skew: 0.361 Prob(JB): 0.153
Kurtosis: 3.331 Cond. No. 86.0
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 5 lags and without small sample correction
因子IC值法
factor_analysis类提供factor_ic_summ方法,支持信息系数(Information Coefficient, IC)方法验证因子有效性,包括因子提纯、计算因子IC值、因子IC值序列检验等。在利用IC值评价因子有效性前,factor_ic_cmpt默认会预先对因子进行提纯,排除行业、市值等重要因素的影响。在每个截面期上,测试因子作为响应变量对市值因子及行业因子做线性回归,取残差作为测试因子的替代值,即可消除因子在行业、市值等方面的偏离。在计算IC值时,factor_ic_cmpt采用更具鲁棒性的秩相关系数(Spearman Rank Correlation)计算每一期初个股因子暴露(剔除行业与市值后)与其到期末的收益率之间的相关性。获取IC值序列后,factor_ic_summ方法将用于计算与IC值相关的指标,从而判断因子的有效性和预测能力。
接口:factor_ic_summ
描述:利用信息系数检验因子是否预测不同股票之间的收益率差异。
输入参数:
| 名称 | 类型 | 必选 | 描述 |
|---|---|---|---|
industry_neutral |
bool | Y | 是否行业中性化,默认为True; |
mkt_cap_neutral |
bool | Y | 是否市值中性化,默认为True |
输出参数:
信息系数评估结果梗概,包含不同换仓期的平均信息系数、信息系数标准差、信息系数显著概率、方向一致性与信息比率等统计量。
使用样例
# statistics on adjusted rank IC series
fa.factor_ic_summ(industry_neutral=True,mkt_cap_neutral=True)
Rank Information Correlation Summary
======================================================
Start Date: 2010-01-01 Mean IC: -0.0959
End Date: 2021-11-01 Std IC: 0.0814
Frequency: Monthly Prob. Significant IC: 0.9161
No. Turnover: 143 Prob. IC > 0: 0.1189
Information Ratio: -1.1782
------------------------------------------------------
投资组合排序法
factor_analysis类提供 quantile_returns_cmpt,quantile_returns_plot与 quantile_returns_summ方法,将根据因子对应公司特征值对股票进行排序,构建投资组合回测,并通过统计指标与可视化方法评价各投资组合表现。在计算投资组合收益率时,quantile_returns_cmpt方法采取流通市值加权方法计算投资组合每期收益率。quantile_returns_summ方法将利用t-值、年化收益率、累计收益率、年化波动率、最大回测、夏普比率等指标评价各投资组合在回测区间内的表现。quantile_return_plot方法将绘制各投资组合在回测期内的累计收益率曲线。
回测表现评价指标
接口:quantile_returns_summ
描述:利用投资组合排序法检验因子是否预测不同股票之间的收益率差异,返回不同投资组合在回测期表现的评价指标。
输入参数:无
输出参数:
投资组合排序法评估结果梗概,包含t-值、年化收益率、累计收益率、年化波动率、最大回测、夏普比率等指标评价各投资组合在回测区间内的表现。
使用样例
fa.quantile_returns_summ()
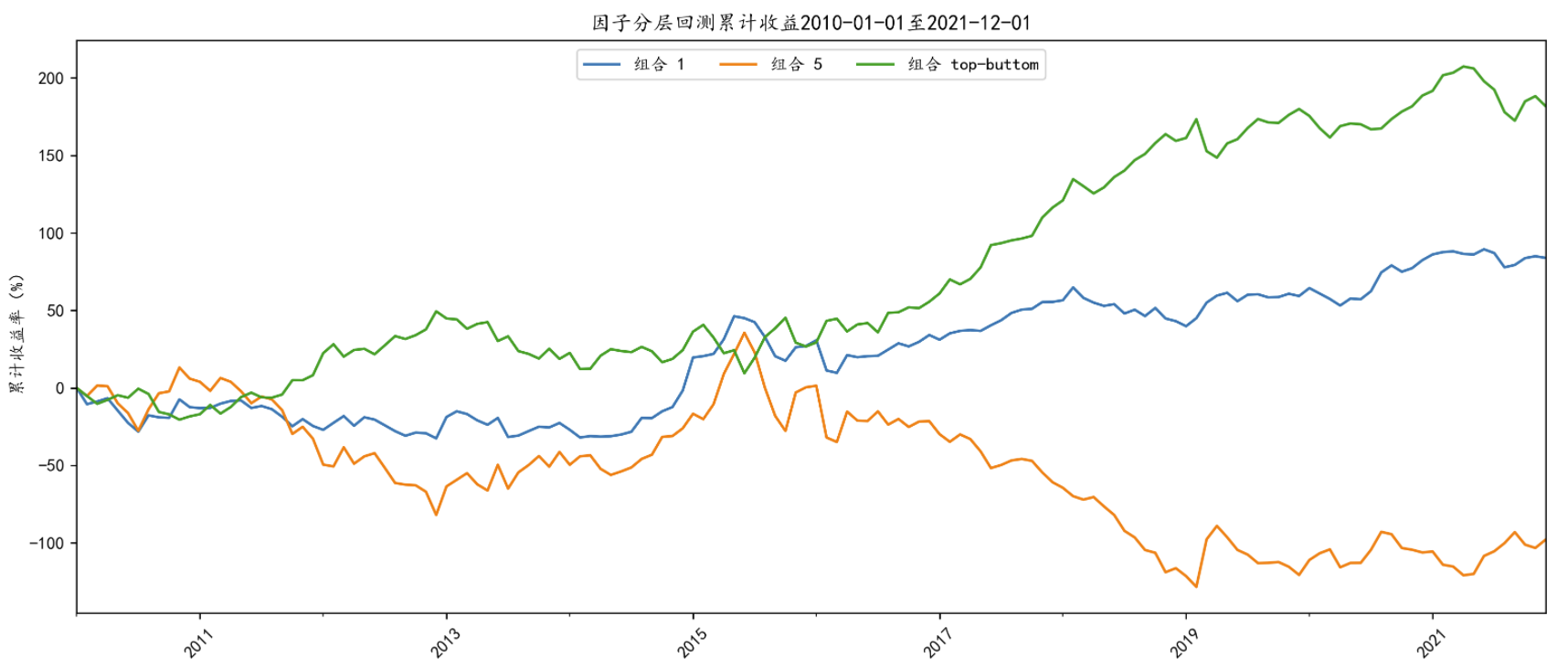
累计收益率曲线
接口:quantile_returns_plot
描述:利用投资组合排序法检验因子是否预测不同股票之间的收益率差异,绘制不同投资组合的累计收益率曲线。
输入参数:
| 名称 | 类型 | 必选 | 描述 |
|---|---|---|---|
plot_type |
str | Y | 绘制曲线类型,默认为‘longshort’,即绘制top组、buttom组和long-short组的累计收益率曲线;可选’all_quantiles’,即绘制所有分位数组别的累计收益率曲线 |
输出参数:
回测期内分位数投资组合累计收益率曲线。
使用样例:
fa.quantile_returns_plot(plot_type = 'longshort')